12 Multilevel PSA
12.1 Introduction
Given the large amount of data to be summarized, the use of graphics are an integral component of representing the results. Pruzek and Helmreich (2009) introduced a class of graphics for visualizing dependent sample tests (see also Pruzek & Helmreich, 2010; Danielak, Pruzek, Doane, Helmreich, & Bryer, 2011). This framework was then extended for propensity score methods using stratification (Helmreich & Pruzek, 2009). In particular, the representation of confidence intervals relative to the unit line (i.e. the line y=x) provided a new way of determining whether there is a statistically significant difference between two groups. The multilevelPSA package provides a number of graphing functions that extend these frameworks for multilevel PSA. The figure below represents a multilevel PSA assessment plot with annotations. This graphic represents the results of comparing private and public schools in North America using the Programme of International Student Assessment (PISA; Organisation for Economic Co-Operation and Development, 2009). The PISA data to create this graphic are included in the multilevelPSA package and a more detailed description of how to create this graphic are discussed in the next section. Additionally, the use of PISA makes more visible certain features of the graphics used. As discussed in chapters four and five, the differences between charter and traditional public schools is minimal and therefore some features of the figures are less apparent. The following section focuses on the features of this graphic.
In the figure below, the x-axis corresponds to math scores for private schools and the y-axis corresponds to public school maths cores. Each colored circle (a) is a country with its size corresponding to the number of students sampled within each country. Each country is projected to the lower left, parallel to the unit line, such that a tick mark is placed on the line with slope -1 (b). These tick marks represent the distribution of differences between private and public schools across countries. Differences are aggregated (and weighted by size) across countries. For math, the overall adjusted mean for private schools is 487, and the overall adjusted mean for public schools is 459 and represented by the horizontal (c) and vertical (d) blue lines, respectively. The dashed blue line parallel to the unit line (e) corresponds to the overall adjusted mean difference and likewise, the dashed green lines (f) correspond to the confidence interval. Lastly, rug plots along the right and top edges of the graphic (g) correspond to the distribution of each country’s overall mean private and public school math scores, respectively.
The figure represents a large amount of data and provides insight into the data and results. The figure provides overall results that would be present in a traditional table, for instance the fact that the green dashed lines do not span the unit line (i.e. y = x) indicates that there is a statistically significant difference between the two groups. However additional information is difficult to convey in tabular format. For example, the rug plots indicate that the spread in the performance of both private and public schools across countries is large. Also observe that Canada, which has the largest PISA scores for both groups, also has the largest difference (in favor of private schools) as represented by the larger distance from the unit line.
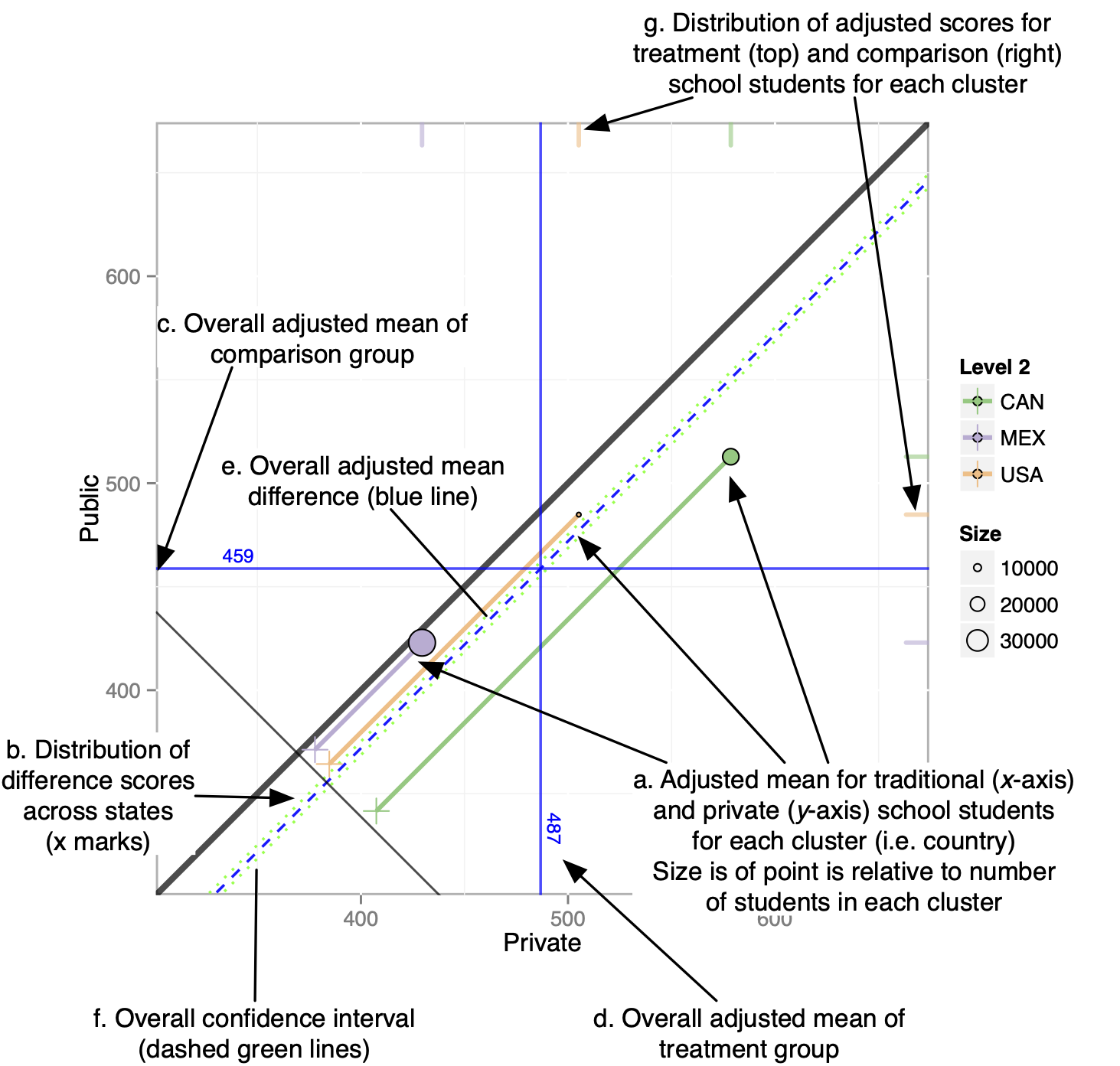
Figure 12.1: Annotated multilevel PSA assessment plot. This plot compares private schools (x- axis) against public schools (y-axis) for North America from the Programme of International Student Assessment.
12.2 Working Example
The multilevelPSA package includes North American data from the Programme of International Student Assessment (PISA; Organisation for Economic Co-Operation and Development, 2009). This data is made freely available for research and is utilized here so that the R code is reproducible9. This example compares the performance of private and public schools clustered by country. Note that PISA provide five plausible values for the academic scores since students complete a subset of the total assessment. For simplicity, the math score used for analysis is the average of these five plausible scores.
data(pisana)
data(pisa.psa.cols)
pisana$MathScore <- apply(pisana[,paste0('PV', 1:5, 'MATH')], 1, sum) / 5The mlpsa.ctree function performs phase I of the propensity score analysis using classification trees, specifically using the ctree function in the party package. The getStrata function returns a data frame with a number of rows equivalent to the original data frame indicating the stratum for each student.
mlpsa <- mlpsa.ctree(pisana[,c('CNT', 'PUBPRIV', pisa.psa.cols)],
formula = PUBPRIV ~ .,
level2 = 'CNT')
mlpsa.df <- getStrata(mlpsa, pisana, level2 = 'CNT')Similarly, the mlpsa.logistic estimates propensity scores using logistic regression. The getPropensityScores function returns a data frame with a number of rows equivalent to the original data frame.
mlpsa.lr <- mlpsa.logistic(pisana[,c('CNT', 'PUBPRIV', pisa.psa.cols)],
formula = PUBPRIV ~ .,
level2 = 'CNT')
mlpsa.lr.df <- getPropensityScores(mlpsa.lr, nStrata = 5)
head(mlpsa.lr.df)## level2 ps strata
## 1 CAN 0.9171885 2
## 2 CAN 0.9410543 3
## 3 CAN 0.9694831 4
## 4 CAN 0.9300448 2
## 5 CAN 0.8362229 1
## 6 CAN 0.9734376 4The covariate.balance function calculates balance statistics for each covariate by estimating the effect of each covariate before and after adjustment. The results can be converted to a data frame to view numeric results or the plot function provides a balance plot. This figure depicts the effect size of each covariate before (blue triangle) and after (red circle) propensity score adjustment. As shown here, the effect size for nearly all covariates is smaller than the unadjusted effect size. The few exceptions are for covariates where the unadjusted effect size was already small. There is no established threshold for what is considered a sufficiently small effect size. In general, I recommend adjusted effect sizes less than 0.1 which reflect less than 1% of variance explained.
cv.bal <- covariate.balance(covariates = pisana[,pisa.psa.cols],
treatment = pisana$PUBPRIV,
level2 = pisana$CNT,
strata = mlpsa.df$strata)
head(as.data.frame(cv.bal))## covariate es.adj es.adj.wtd es.unadj
## 1 (Intercept) 0.00000000 0.000000e+00 NaN
## 2 ST05Q01Yes, more than one year 0.09720705 2.335610e-04 0.28695986
## 3 ST05Q01Yes, one year or less 0.05131164 6.622276e-05 0.22032056
## 4 ST07Q01Yes, once 0.10349619 -1.123270e-03 0.23453956
## 5 ST07Q01Yes, twice or more 0.04447145 -3.720711e-04 0.08655983
## 6 ST10Q01<ISCED level 2> 0.02969316 -1.733254e-04 0.17085288
plot(cv.bal)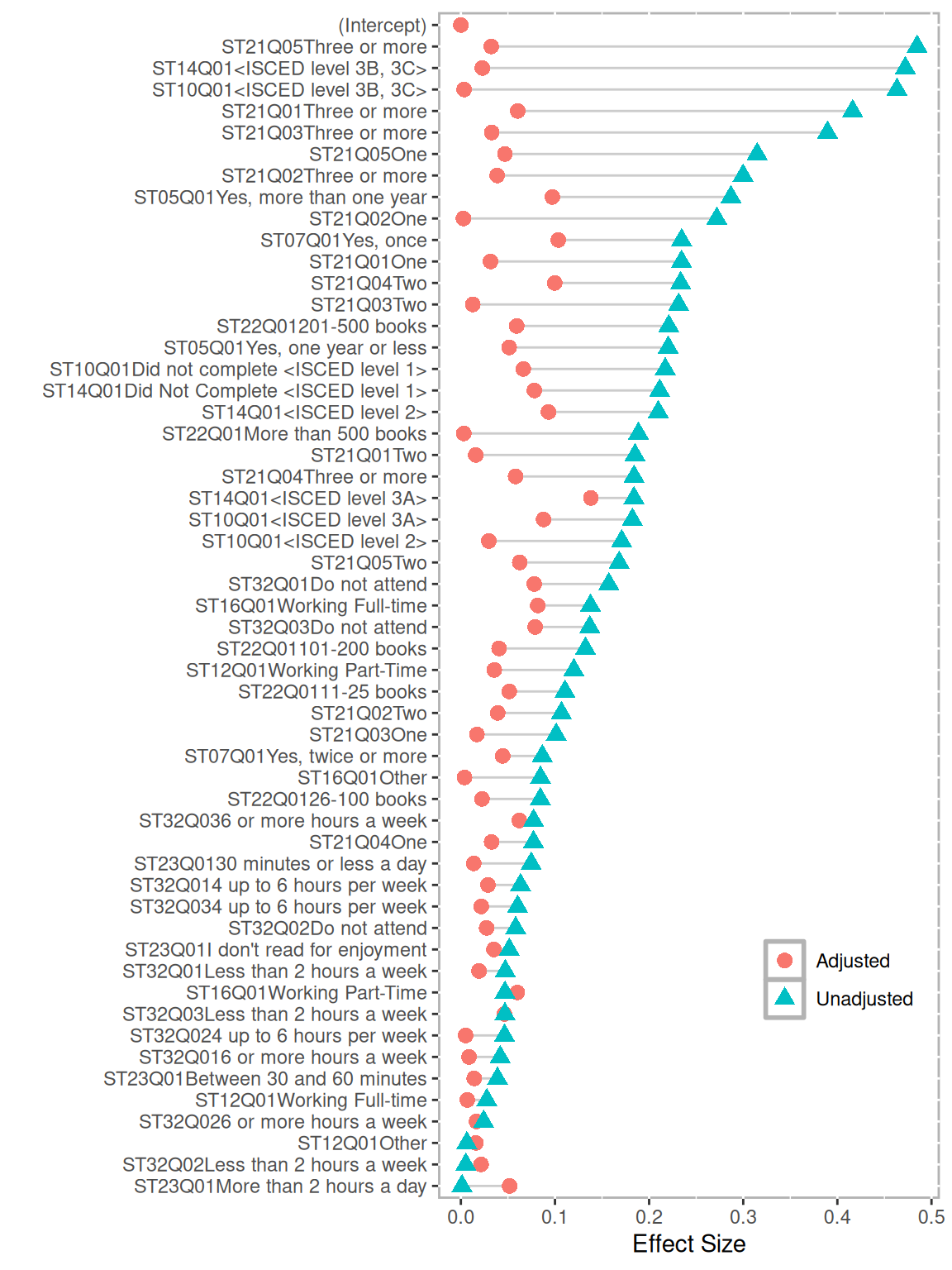
Figure 12.2: Multilevel PSA balance plot for PISA. The effect sizes (standardized mean differences) for each covariate are provided before PSA adjustment (blue triangles) and after PSA adjustment (red circles).
The mlpsa function performs phase II of propensity score analysis and requires four parameters: the response variable, treatment indicator, stratum, and clustering indicator. The minN parameter (which defaults to five) indicates what the minimum stratum size is to be included in the analysis. For this example, 463, or less than one percent of students were removed because the stratum (or leaf node for classification trees) did not contain at least five students from both the treatment and control groups.
results.psa.math <- mlpsa(response = mlpsa.df$MathScore,
treatment = mlpsa.df$PUBPRIV,
strata = mlpsa.df$strata,
level2 = mlpsa.df$CNT)The summary function provides the overall treatment estimates as well as level one and two summaries.
summary(results.psa.math)## level2 strata Treat Treat.n Control Control.n ci.min ci.max
## 1 CAN Overall 578.6262 1625 512.7997 21093 -72.08031 -59.572751
## 2 <NA> 1 580.0069 28 491.6351 1128 NA NA
## 3 <NA> 2 599.9024 9 476.2717 1326 NA NA
## 4 <NA> 3 585.2667 11 512.7478 630 NA NA
## 5 <NA> 4 570.6395 140 508.2071 2240 NA NA
## 6 <NA> 5 578.2330 8 470.1353 179 NA NA
## 7 <NA> 6 499.9746 19 447.4332 310 NA NA
## 8 <NA> 7 584.4352 83 503.0039 3276 NA NA
## 9 <NA> 8 471.0636 5 464.1163 120 NA NA
## 10 <NA> 9 559.6253 41 525.9859 190 NA NA
## 11 <NA> 10 501.7639 20 463.2017 91 NA NA
## 12 <NA> 11 556.9058 44 516.6588 750 NA NA
## 13 <NA> 12 559.2598 34 520.6171 292 NA NA
## 14 <NA> 13 561.9538 8 489.0613 475 NA NA
## 15 <NA> 14 533.6619 21 463.1110 151 NA NA
## 16 <NA> 15 584.6585 126 519.8063 2134 NA NA
## 17 <NA> 16 565.9650 25 532.7037 245 NA NA
## 18 <NA> 17 613.4358 49 576.0543 137 NA NA
## 19 <NA> 18 563.2071 57 526.8732 659 NA NA
## 20 <NA> 19 598.0457 113 541.9625 318 NA NA
## 21 <NA> 20 629.1768 15 561.7597 143 NA NA
## 22 <NA> 21 588.7047 46 522.5698 398 NA NA
## 23 <NA> 22 594.4176 99 548.0534 194 NA NA
## 24 <NA> 23 579.9481 40 542.2590 183 NA NA
## 25 <NA> 24 581.4634 52 539.2326 342 NA NA
## 26 <NA> 25 582.1617 103 525.7403 1219 NA NA
## 27 <NA> 26 625.7713 11 525.2688 113 NA NA
## 28 <NA> 27 589.4497 35 516.2204 804 NA NA
## 29 <NA> 28 524.1864 5 482.3364 15 NA NA
## 30 <NA> 29 551.1838 12 526.8786 348 NA NA
## 31 <NA> 30 588.0390 145 526.4254 1195 NA NA
## 32 <NA> 31 602.9849 147 545.2503 822 NA NA
## 33 <NA> 32 528.0377 27 528.4283 7 NA NA
## 34 <NA> 33 552.0727 47 510.3964 659 NA NA
## 35 MEX Overall 429.5247 4044 422.9746 34090 -10.04346 -3.056743
## 36 <NA> 1 516.4931 83 485.4115 13 NA NA
## 37 <NA> 2 491.4609 145 447.6702 89 NA NA
## 38 <NA> 3 494.1497 151 475.4165 178 NA NA
## 39 <NA> 4 417.9966 14 415.7178 154 NA NA
## 40 <NA> 5 453.8781 127 438.1276 484 NA NA
## 41 <NA> 6 452.5168 58 431.0051 635 NA NA
## 42 <NA> 7 496.4715 247 486.7400 293 NA NA
## 43 <NA> 8 483.2088 431 461.4194 871 NA NA
## 44 <NA> 9 472.3820 6 466.6849 110 NA NA
## 45 <NA> 10 460.6080 16 449.7257 121 NA NA
## 46 <NA> 11 481.4797 285 470.4227 696 NA NA
## 47 <NA> 12 474.0785 16 442.7985 112 NA NA
## 48 <NA> 13 405.3955 33 413.0509 943 NA NA
## 49 <NA> 14 431.6230 138 429.0045 1484 NA NA
## 50 <NA> 15 472.3767 99 459.7159 619 NA NA
## 51 <NA> 16 445.3934 78 437.8734 898 NA NA
## 52 <NA> 17 460.4928 34 461.1886 262 NA NA
## 53 <NA> 18 460.1316 113 454.8656 367 NA NA
## 54 <NA> 19 433.8334 53 444.9685 454 NA NA
## 55 <NA> 20 457.9868 69 445.7740 367 NA NA
## 56 <NA> 21 461.7578 76 457.0506 217 NA NA
## 57 <NA> 22 477.1849 93 452.3768 150 NA NA
## 58 <NA> 23 475.5367 186 459.6453 547 NA NA
## 59 <NA> 24 476.8898 10 437.3241 130 NA NA
## 60 <NA> 25 475.5922 80 441.7604 159 NA NA
## 61 <NA> 26 436.7231 167 427.7595 1040 NA NA
## 62 <NA> 27 436.3677 146 434.9281 1175 NA NA
## 63 <NA> 28 441.9648 45 428.9776 406 NA NA
## 64 <NA> 29 424.4490 80 428.0604 1963 NA NA
## 65 <NA> 30 436.0249 61 426.6096 787 NA NA
## 66 <NA> 31 426.2893 48 427.6944 645 NA NA
## 67 <NA> 32 400.6292 231 409.2472 4314 NA NA
## 68 <NA> 33 442.1996 28 437.6917 279 NA NA
## 69 <NA> 34 423.5202 34 426.4274 1013 NA NA
## 70 <NA> 35 419.9079 63 427.3862 2364 NA NA
## 71 <NA> 36 408.3097 18 400.4286 234 NA NA
## 72 <NA> 37 406.4552 107 397.2436 3632 NA NA
## 73 <NA> 38 424.5754 25 411.6970 2434 NA NA
## 74 <NA> 39 448.6755 15 431.5050 342 NA NA
## 75 <NA> 40 362.4143 7 348.4556 1959 NA NA
## 76 <NA> 41 381.2044 15 346.2349 1004 NA NA
## 77 <NA> 42 510.2599 313 487.5493 146 NA NA
## 78 USA Overall 505.2189 345 484.8212 4888 -32.03916 -8.756334
## 79 <NA> 1 479.2228 50 475.0463 1219 NA NA
## 80 <NA> 2 490.3678 16 447.5507 1323 NA NA
## 81 <NA> 3 501.7149 34 487.6484 462 NA NA
## 82 <NA> 4 528.1903 42 506.7805 263 NA NA
## 83 <NA> 5 511.8919 42 502.8831 335 NA NA
## 84 <NA> 6 519.6260 21 476.6840 526 NA NA
## 85 <NA> 7 565.4985 80 558.6464 278 NA NA
## 86 <NA> 8 560.4173 41 541.0285 207 NA NA
## 87 <NA> 9 511.0133 14 528.7377 259 NA NA
## 88 <NA> 10 522.3160 5 460.6910 16 NA NAThe plot function creates the multilevel assessment plot. Here it is depicted with side panels showing the distribution of math scores for all strata for public school students to the left and private school students below. These panels can be plotted separately using the mlpsa.circ.plot and mlpsa.distribution.plot functions.
plot(results.psa.math)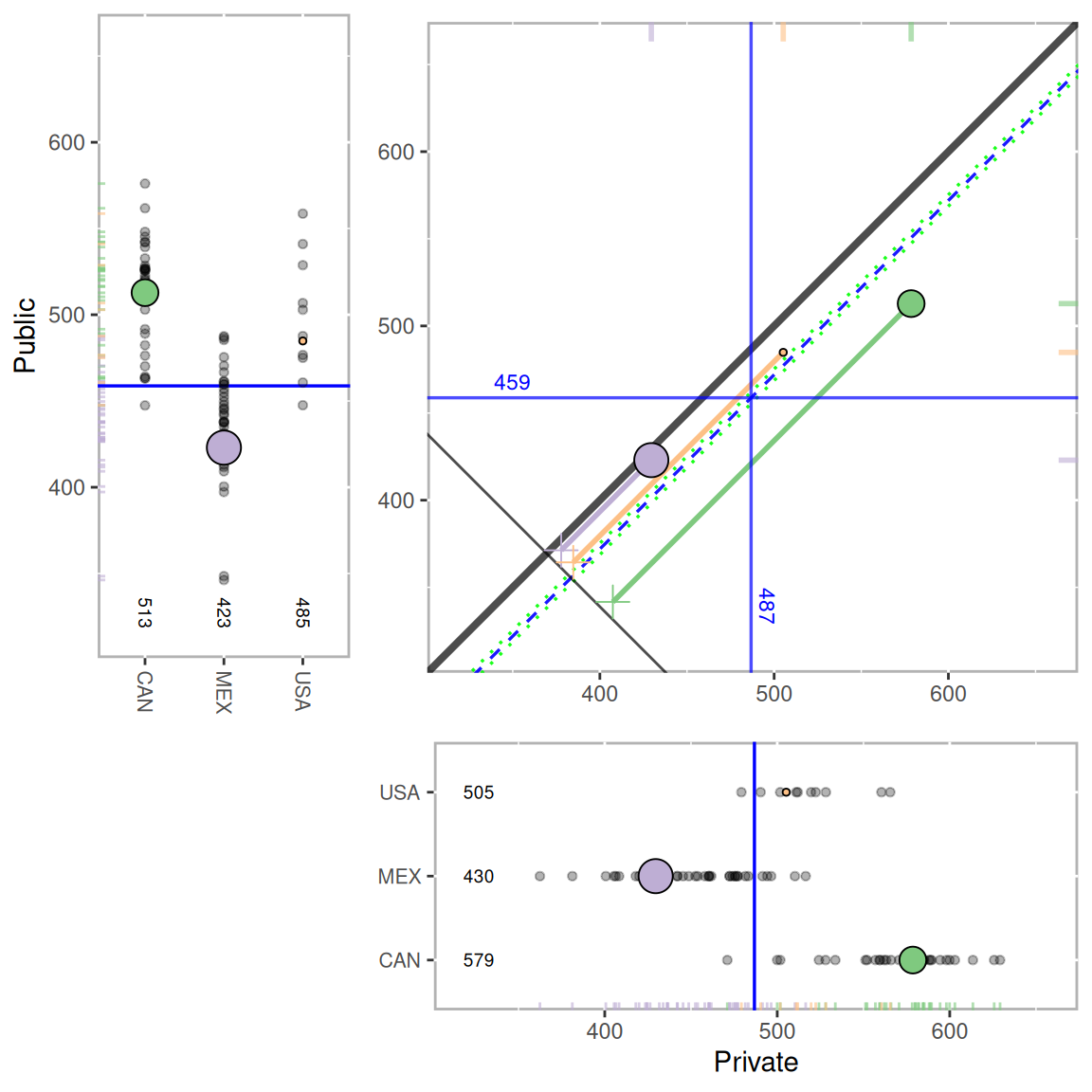
Figure 12.3: Multilevel PSA assessment plot for PISA. The main panel provides the adjusted mean for private (x-axis) and public (y-axis) for each country. The left and lower panels provide the mean for each stratum for the public and private students, respectively. The overall adjusted mean difference is represented by the dashed blue line and the 95% confidence interval by the dashed green lines. There is a statistically significant difference between private and public school student performance as evidenced by the confidence interval not spanning zero (i.e. not crossing the unit line y=x.
Lastly, the mlpsa.difference.plot function plots the overall differences. The sd parameter is optional, but if specified, the x-axis can be interpreted as standardized effect sizes.
mlpsa.difference.plot(results.psa.math,
sd = mean(mlpsa.df$MathScore, na.rm=TRUE))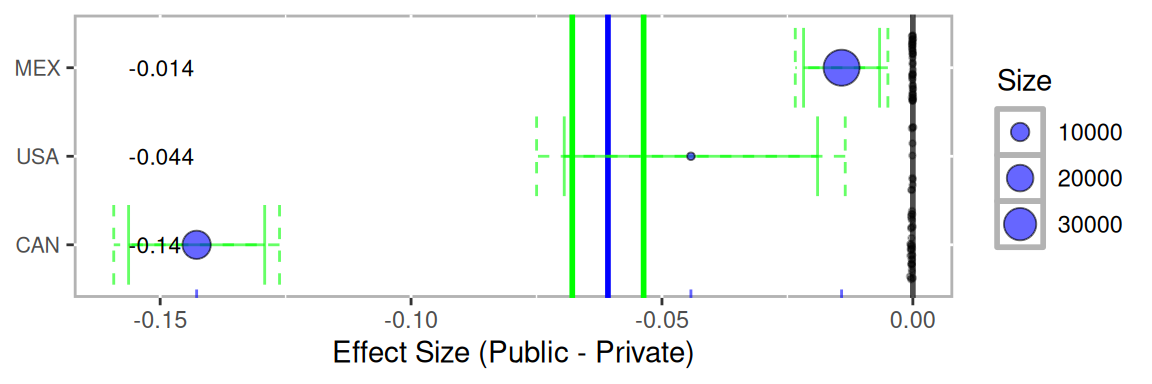
Figure 12.4: Multilevel PSA difference plot for PISA. Each blue dot corresponds to the effect size (standardized mean difference) for each country. The vertical blue line corresponds to the overall effect size for all countries. The green lines correspond to the 95% confidence intervals. The dashed green lines Bonferroni-Sidak (c.f. Abdi, 2007) adjusted confidence intervals. The size of each dot is proportional to the sample size within each country.